【算法】链表

本文介绍了链表类型经典算法的学习记录
合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
提示:
• 两个链表的节点数目范围是 [0, 50]
• -100 <= Node.val <= 100
• l1 和 l2 均按 非递减顺序 排列
思路
将其当作模拟题,新建一个头,将两个链表挨个遍历,比较大小,将较小的一个添加进新链表,再往后移动。
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode* p = list1;
ListNode* q = list2;
if(p == nullptr){
return q;
}
if(q == nullptr){
return p;
}
// 选定p为基准
ListNode* newHead = new ListNode(0,nullptr);
ListNode* x = newHead;
while(p!= nullptr || q != nullptr){
if(p!= nullptr){
if(q == nullptr || p->val <= q->val){
x->next = p;
p = p->next;
x = x->next;
}
}
if(q!= nullptr){
if(p == nullptr || q->val < p->val){
x->next = q;
q = q->next;
x = x->next;
}
}
}
return newHead->next;
}
};
官方题解
使用递归算法,设置一个比较函数,同时判断两个链表的头,每次都将更小的节点的next保留,再次调用比较函数,最后一层一层返回这个结果。也就是说,两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。
我们直接将以上递归过程建模,同时需要考虑边界情况。 如果 l1 或者 l2 一开始就是空链表 ,那么没有任何操作需要合并,所以我们只需要返回非空链表。否则,我们要判断 l1 和 l2 哪一个链表的头节点的值更小,然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空,递归结束。
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
// list1已经遍历完,剩下的list2为更大的数字,直接加在尾部
if (list1 == nullptr) {
return list2;
} else if (list2 == nullptr) {
return list1;
} else if (list1->val < list2->val) {
// list1的值更小,保留list1这个元素的next指针,指向后面的更大的元素
list1->next = mergeTwoLists(list1->next, list2);
return list1;
} else {
list2->next = mergeTwoLists(list1, list2->next);
return list2;
}
}
找到两个相交链表的交点节点
给定两个单链表的头节点 headA 和 headB ,请找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须保持其原始结构 。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
思路1 判断共尾节点计算差值
先判断二者中有无空链表;两个链表相交必是同一个尾节点;计算是否共尾节点,同时计算出各自的长度,比较出长度差,将较长的那个先移动这个差值的距离,然后两个链表再一起移动,两个指针就会慢慢指向同节点,判断相等了返回即可。
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if(headA == nullptr || headB == nullptr){
return nullptr;
}
ListNode *p = headA;
ListNode *q = headB;
int lenthA = 0;
int lenthB = 0;
while(p->next != nullptr) {
p = p->next;
lenthA++;
}
while(q->next != nullptr) {
q = q->next;
lenthB++;
}
if(p != q){
return nullptr;
}
p = headA;
q = headB;
if(lenthA > lenthB){
int diff = lenthA-lenthB;
while(diff>0){
p = p->next;
diff--;
}
}
if(lenthA < lenthB){
int diff = lenthB-lenthA;
while(diff>0){
q = q->next;
diff--;
}
}
while(p != q){
p = p->next;
q = q->next;
}
return p;
}
};
思路2 hash集合 unordered_set
判断两个链表是否相交,可以使用哈希集合存储链表节点。
首先遍历链表 headA,并将链表 headA 中的每个节点加入哈希集合中。然后遍历链表 headB,对于遍历到的每个节点,判断该节点是否在哈希集合中:
如果当前节点不在哈希集合中,则继续遍历下一个节点;
如果当前节点在哈希集合中,则后面的节点都在哈希集合中,即从当前节点开始的所有节点都在两个链表的相交部分,因此 在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点,返回该节点 。
如果链表 headB 中的所有节点都不在哈希集合中,则两个链表不相交,返回 null。
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
unordered_set<ListNode *> visited;
ListNode *temp = headA;
while (temp != nullptr) {
visited.insert(temp);
temp = temp->next;
}
temp = headB;
while (temp != nullptr) {
if (visited.count(temp)) {
return temp;
}
temp = temp->next;
}
return nullptr;
}
};
翻转链表
给定单链表的头节点 head ,请反转链表,并返回反转后的链表的头节点。
示例 1:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
• 链表中节点的数目范围是 [0, 5000]
• -5000 <= Node.val <= 5000
进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
思路
使用栈来暂存所有数据,出栈的时候新建一个头节点,来创建逆序链表。
使用 stack 容器处理,空间复杂度O(n)
ListNode* reverseList(ListNode* head) {
stack<int> temp;
ListNode * p = head;
while(p != nullptr){
cout<<"value: "<<p->val<<endl;
temp.push(p->val);
p = p->next;
}
ListNode* newHead = new ListNode();
ListNode* q = newHead;
while(!temp.empty()){
cout<<"stack value: "<<temp.top()<<endl;
ListNode* tempNode = new ListNode(temp.top());
q->next = tempNode;
q = q->next;
temp.pop();
}
return newHead->next;
}
思路2
官方题解,遍历链表,使用两个指针来保存当前值和上一个的值,同时在循环中需要暂时存储下一个节点地址,防止断链。 循环时,将当前节点的next节点的next指针指向当前节点,当前节点的next指针指向上一个节点,然后当前节点和上一个节点都往后走。
// 只用了两个变量,空间复杂度 O(1)
ListNode* reverseList2(ListNode* head) {
ListNode * current = head;
ListNode * prev = nullptr;
while (current != nullptr) {
ListNode * next = current->next;
current->next = prev;
prev = current;
current = next;
}
return prev;
}
思路3 官方的递归解法
递归版本稍微复杂一些,其关键在于反向工作。假设链表的其余部分已经被反转,现在应该如何反转它前面的部分?
假设链表为: n1 →…→ nk−1 → nk → nk+1 →…→ nm →∅
若从节点 nk+1 到 nm 已经被反转,而我们正处于 nk 。
n1 →…→ nk−1 → nk →nk+1 ←…← nm
我们希望 nk+1 的下一个节点指向 nk。
所以,nk.next.next=nk 。需要注意的是 n1 的下一个节点必须指向 ∅。如果忽略了这一点,链表中可能会产生环.
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (!head || !head->next) {
return head;
}
ListNode* newHead = reverseList(head->next);
head->next->next = head;
head->next = nullptr;
return newHead;
}
};
翻转链表2
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例 1:
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
示例 2:
输入:head = [5], left = 1, right = 1
输出:[5]
提示:
• 链表中节点数目为 n
• 1 <= n <= 500
• -500 <= Node.val <= 500
• 1 <= left <= right <= n
进阶: 你可以使用一趟扫描完成反转吗?
思路1 掐断 翻转 拼接
将要反转的区间掐断,采用上一题的方法来翻转,关键 提前存储好区间左侧和右侧的第一个节点 ,方便再拼接回去,但是注意这里可能并没有前一个节点,所以加一个虚拟头节点,来承接翻转后的区间,免去多余判断。区间右侧的第一个节点为nullptr没有关系。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* current = head;
ListNode* priv = nullptr;
while (current != nullptr) {
ListNode* next = current->next;
current->next = priv;
priv = current;
current = next;
}
return priv;
}
ListNode* reverseBetween(ListNode* head, int left, int right) {
if (left == right) {
return head;
}
ListNode* dummyHead = new ListNode(-1);
dummyHead->next = head;
ListNode* p = dummyHead;
ListNode* q = dummyHead;
ListNode* first;
ListNode* last;
for (int i = 0; i < left - 1; i++) {
p = p->next;
}
first = p->next;
for (int j = 0; j < right; j++) {
q = q->next;
}
last = q;
// 将q移到区间外第一个元素位置
q = q->next;
p->next = last;
last->next = nullptr;
ListNode* corridor = reverseList(first);
while (corridor->next != nullptr) {
corridor = corridor->next;
}
corridor->next = q;
return dummyHead->next;
}
};
思路2 穿针引线
方法一的缺点是:如果 left 和 right 的区域很大,恰好是链表的头节点和尾节点时,找到 left 和 right 需要遍历一次,反转它们之间的链表还需要遍历一次,虽然总的时间复杂度为 O(N),但 遍历了链表 2 次 ,可不可以只遍历一次呢?答案是可以的。
在需要反转的区间里,每遍历到一个节点,让这个新节点来到反转部分的起始位置。下面的图展示了整个流程。
初始链表:9->7->2->5->4->3->6 第一步将5插到2的前面,第二步将4插到2的前面。。。
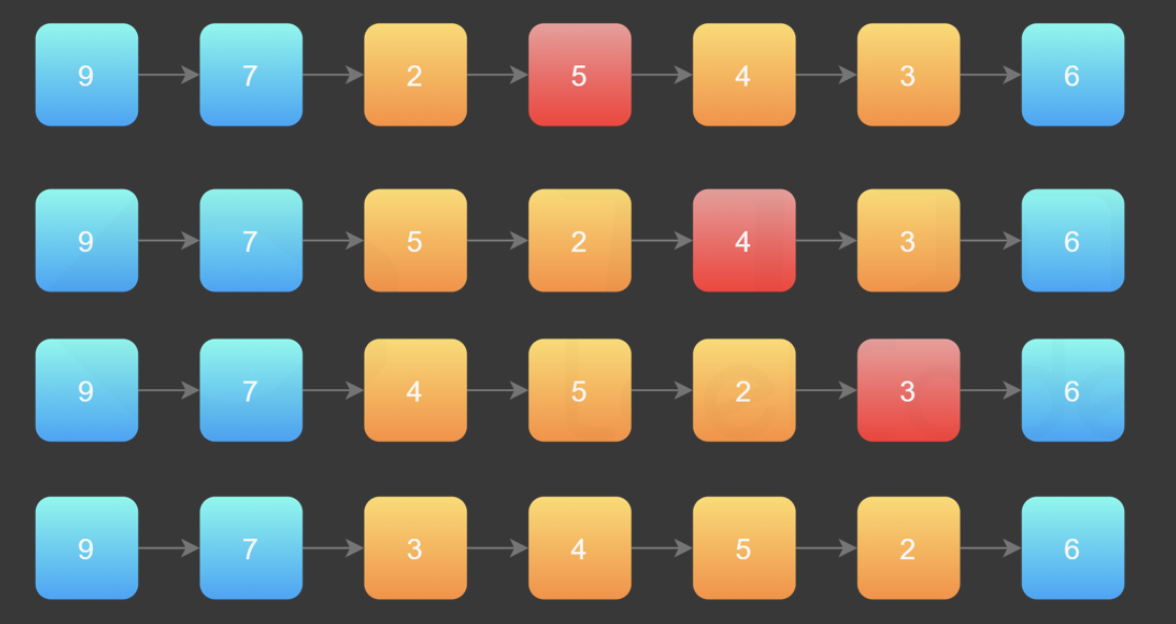
使用三个指针变量 pre、curr、next 来记录反转的过程中需要的变量,它们的意义如下:
- curr:指向待反转区域的第一个节点 left;
- next:永远指向 curr 的下一个节点,循环过程中,curr 变化以后 next 会变化;
- pre:永远指向待反转区域的第一个节点 left 的前一个节点,在循环过程中不变。
class Solution {
public:
ListNode *reverseBetween(ListNode *head, int left, int right) {
// 设置虚拟头节点,用于处理头节点可能被翻转的情况
// 这是处理链表问题的常用技巧,可以避免对头节点的特殊处理
ListNode *dummyNode = new ListNode(-1);
dummyNode->next = head;
// pre指针指向要翻转区间的前一个节点
// 通过循环将pre移动到left位置的前一个节点
ListNode *pre = dummyNode;
for (int i = 0; i < left - 1; i++) {
pre = pre->next;
}
// cur指针指向当前要处理的节点(翻转区间的第一个节点)
ListNode *cur = pre->next;
ListNode *next; // 用于临时存储下一个要处理的节点
// 进行区间内的节点翻转
// 循环次数为区间长度减1(right - left)
for (int i = 0; i < right - left; i++) {
// next指向cur的下一个节点(即要移动到前面的节点)
next = cur->next;
// 将cur指向next的下一个节点,跳过next节点
cur->next = next->next;
// 将next节点插入到pre节点的后面
next->next = pre->next;
// 更新pre的next指针,指向新插入到前面的next节点
pre->next = next;
}
// 返回虚拟头节点的下一个节点(即新的头节点)
return dummyNode->next;
}
};
翻转链表3(k个一组)
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
示例 2:
输入:head = [1,2,3,4,5], k = 3
输出:[3,2,1,4,5]
提示:
• 链表中的节点数目为 n
• 1 <= k <= n <= 5000
• 0 <= Node.val <= 1000
进阶:你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗?
思路
基于 1 & 2 版本,更需要控制好每一组之间的链接,尤其是循环后的翻转和善后工作。
记录了区间的头尾,区间的上一个,还有区间的下一个,用于断链后重新链接翻转后的区间。有别于官方题解,本地编译器用不了pair等C++11以后的库,所以区间翻转后,是通过移动区间头指针来找到翻转后的区间尾节点,来链接下一个点的。
class Solution {
public:
ListNode *reverseList(ListNode *head)
{
ListNode *current = head;
ListNode *priv = nullptr;
while (current != nullptr)
{
ListNode *next = current->next;
current->next = priv;
priv = current;
current = next;
}
return priv;
}
ListNode *reverseKGroup(ListNode *head, int k)
{
ListNode *dummyHead = new ListNode(-1);
dummyHead->next = head;
ListNode *priv;
ListNode *p = dummyHead;
while (p != nullptr)
{
priv = p;
ListNode *reverseHead = priv->next;
for (int i = 0; i < k; i++)
{
p = p->next;
if (p == nullptr)
{
return dummyHead->next;
}
}
ListNode *reverseTail = p;
ListNode *nextNode = p->next;
reverseTail->next = nullptr;
ListNode *reversed = reverseList(reverseHead);
priv->next = reversed;
while (reversed->next != nullptr)
{
reversed = reversed->next;
}
p = reversed;
reversed->next = nextNode;
}
return dummyHead->next;
}
};
复制带随机指针的链表
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。
示例 1:
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:
输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3:
输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
提示:
• 0 <= n <= 1000
• -104 <= Node.val <= 104
• Node.random 为 null 或指向链表中的节点。
思路1
使用一个map,键为原始链表节点 A ,值为新建的节点 A’ ,在遍历原始链表的时候,看看原始节点的指针指向了哪里,通过map寻找对应节点key的value,就可以完全复制。
class Solution {
public:
Node* copyRandomList(Node* head) {
unordered_map<Node*, Node*> nodeMap;
Node* p = head;
while(p!=nullptr){
nodeMap[p] = new Node(p->val);
p = p->next;
}
p = head;
while(p!=nullptr){
// 映射的next等于next的映射
nodeMap[p]->next = nodeMap[p->next];
nodeMap[p]->random = nodeMap[p->random];
p = p->next;
}
return nodeMap[head];
}
};
缺点:
使用了多一个的map空间,需要遍历两次,先添加一次,再根据映射关系来设置指向关系。
官方优化
一样使用了哈希表,但是使用了回溯算法,在第一个节点检查时就去创建指向的两个节点,如果为未创建过就新建一个填进map,如果已创建就不能再刷新value来了,而是直接复用这个值。少遍历了一遍执行时间从11ms,优化到了8ms。
class Solution {
public:
unordered_map<Node*, Node*> cachedNode;
Node* copyRandomList(Node* head) {
if (head == nullptr) {
return nullptr;
}
if (!cachedNode.count(head)) {
Node* headNew = new Node(head->val);
cachedNode[head] = headNew;
headNew->next = copyRandomList(head->next);
headNew->random = copyRandomList(head->random);
}
return cachedNode[head];
}
};
思路2
以上空间复杂度O(n),需要额外使用一个大map来存储节点,我们可以将新节点挨个插到每一个原始节点中间,然后遍历的时候,使用该节点指向原始节点的next指针来寻找刚刚新建的新节点,最后将新节点剥离出来,同时保证原链表正确还原(题目没有提这一点,但是检查的时候应该是需要用到原链表)
Node *copyRandomList(Node *head)
{
// 长度为0
if (head == nullptr)
{
return nullptr;
}
Node *p = head;
// 添加复制节点
while (p)
{
Node *next = p->next;
Node *copyNode = new Node(p->val);
p->next = copyNode;
copyNode->next = next;
p = p->next->next;
}
// 复制各个节点random指针
p = head;
while (p)
{
Node *copyNode = p->next;
if (p->random == nullptr)
{
copyNode->random = nullptr;
}
else
{
copyNode->random = p->random->next;
}
p = p->next->next;
}
// 链表分离出来之后,next指针自动正确了
p = head;
Node *ans = head->next;
Node *q = head->next;
// 当q已经触底,遍历到了最后一个
while (q->next != nullptr)
{
Node *copyNode = q->next->next;
Node *originNode = p->next->next;
q->next = copyNode;
p->next = originNode;
q = copyNode;
p = originNode;
}
// 目前两个链表是共尾节点的状态
// 掐断原始链表的指向复制链表的最后一个节点
p->next = nullptr;
return ans;
}
判断环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
提示:
• 链表中节点的数目范围是 [0, 104]
• -105 <= Node.val <= 105
• pos 为 -1 或者链表中的一个 有效索引 。
进阶:你能用 O(1)(即,常量)内存解决此问题吗?
思路1
使用不可存在相同元素的set数据结构来存储每个节点的next地址,如果有相同的节点地址已经出现过,则说明有环,否则无环;
class Solution {
public:
bool hasCycle(ListNode* head) {
set<ListNode*> tempset;
ListNode* p = head;
tempset.insert(head);
while (p != nullptr) {
if (tempset.count(p->next) > 0) {
return true;
}
tempset.insert(p->next);
p = p->next;
}
return false;
}
};
这种方法空间复杂度为O(n),执行时长也排到了末尾;
思路2
使用快慢指针,快指针一次走两个,慢指针一次走一个,如果能碰到一起,说明肯定有环存在;
bool hasCycle2(ListNode *head)
{
ListNode *fast = head;
ListNode *slow = head;
while (slow != nullptr && fast != nullptr && fast->next != nullptr)
{
slow = slow->next;
fast = fast->next->next;
if (slow == fast)
{
return true;
}
}
return false;
}
优化
while中使用三个判断条件,发现耗时有点长,将快指针的next空判断移到循环内部,可以进一步减少耗时。
class Solution {
public:
bool hasCycle(ListNode* head) {
ListNode* fast = head;
ListNode* slow = head;
while (slow != nullptr && fast != nullptr) {
if (fast->next != nullptr) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
return true;
}
} else {
return false;
}
}
return false;
}
};
找到环形链表的入环节点
给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
说明:不允许修改给定的链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引
进阶:是否可以使用 O(1) 空间解决此题?
思路
还是使用set,当判断存在相同的地址时,直接返回这个节点地址即可。
class Solution {
public:
ListNode* detectCycle(ListNode* head) {
set<ListNode*> tempset;
ListNode* p = head;
tempset.insert(head);
while (p != nullptr) {
if (tempset.count(p->next) > 0) {
return p->next;
}
tempset.insert(p->next);
p = p->next;
}
return nullptr;
}
};
同样多创建了一个空间来存储地址
思路2
这个只需完整记忆,证明过程太复杂。使用快慢指针,当他们相遇时,将快指针还原到头节点。而后,快指针也变成一次跳一步,继续循环,当快慢指针第二次相遇时,就是在入环的节点位置。
class Solution {
public:
ListNode* detectCycle2(ListNode* head) {
ListNode* fast = head;
ListNode* slow = head;
int meet_count = 0;
while (fast != nullptr && slow != nullptr) {
if (fast->next != nullptr) {
slow = slow->next;
if (meet_count == 0) {
fast = fast->next->next;
if (slow == fast) {
fast = head;
meet_count++;
}
} else {
fast = fast->next;
if (slow == fast) {
return fast;
}
}
} else {
return nullptr;
}
}
return nullptr;
}
};
在两个节点互相循环时有问题,可以说是互为入口,index是0,算出来是1.
链表排序
给定链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:
输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:
输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
提示:
• 链表中节点的数目在范围 [0, 5 * 104] 内
• -105 <= Node.val <= 105
进阶:你可以在 O(nlogn) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
思路1
使用multiset,可以添加重复元素,可以自动排序。
class Solution
{
public:
ListNode *sortList(ListNode *head)
{
if (head == nullptr)
{
return head;
}
multiset<int> sort_set;
ListNode *p = head;
while (p != nullptr)
{
sort_set.insert(p->val);
p = p->next;
}
auto iterator = sort_set.begin();
ListNode *newHead = new ListNode(*iterator);
p = newHead;
iterator++;
while (iterator != sort_set.end())
{
ListNode *node = new ListNode(*iterator);
p->next = node;
p = p->next;
iterator++;
}
return newHead;
}
};
性能较差
思路2
自上而下归并排序,不断二分,等颗粒度为1时,使用merge合并两个有序链表(长度为1一定有序),将所有的小链表 merge() 连接起来,最后合成一个大的。
class Solution {
public:
ListNode* sortList(ListNode* head) {
return sortList(head, nullptr);
}
ListNode* sortList(ListNode* head, ListNode* tail) {
if (head == nullptr) {
return head;
}
if (head->next == tail) {
head->next = nullptr;
return head;
}
ListNode* slow = head, *fast = head;
while (fast != tail) {
slow = slow->next;
fast = fast->next;
if (fast != tail) {
fast = fast->next;
}
}
ListNode* mid = slow;
return merge(sortList(head, mid), sortList(mid, tail));
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
时间复杂度:O(nlogn),其中 n 是链表的长度。 空间复杂度:O(logn),其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间。
思路3
自下而上归并排序,步长为1,遍历排序,步长为2,再次排序。
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (head == nullptr) {
return head;
}
int length = 0;
ListNode* node = head;
while (node != nullptr) {
length++;
node = node->next;
}
ListNode* dummyHead = new ListNode(0, head);
for (int subLength = 1; subLength < length; subLength <<= 1) {
ListNode* prev = dummyHead, *curr = dummyHead->next;
while (curr != nullptr) {
ListNode* head1 = curr;
for (int i = 1; i < subLength && curr->next != nullptr; i++) {
curr = curr->next;
}
ListNode* head2 = curr->next;
curr->next = nullptr;
curr = head2;
for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr; i++) {
curr = curr->next;
}
ListNode* next = nullptr;
if (curr != nullptr) {
next = curr->next;
curr->next = nullptr;
}
ListNode* merged = merge(head1, head2);
prev->next = merged;
while (prev->next != nullptr) {
prev = prev->next;
}
curr = next;
}
}
return dummyHead->next;
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
时间复杂度:O(nlogn),其中 n 是链表的长度。 空间复杂度:O(1)。
回文链表判断
给定一个链表的 头节点 head ,请判断其是否为回文链表。
如果一个链表是回文,那么链表节点序列从前往后看和从后往前看是相同的。
示例 1:
输入: head = [1,2,3,3,2,1]
输出: true
示例 2:
输入: head = [1,2]
输出: false
提示:
• 链表 L 的长度范围为 [1, 105]
• 0 <= node.val <= 9
进阶:能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
思路1 使用stack来辅助
回文即正反看起来相同,第一种解法使用栈来压入所有元素,然后弹出栈元素同时遍历链表,看看二者每一个值是否一样。耗时224ms。
class Solution {
public:
bool isPalindrome(ListNode* head) {
ListNode* p = head;
stack<int> temp_stack;
while (p != nullptr) {
temp_stack.push(p->val);
p = p->next;
}
p = head;
while (!temp_stack.empty()) {
if (p->val != temp_stack.top()) {
return false;
}
p = p->next;
temp_stack.pop();
}
return true;
}
};
思路2 快慢指针找中点,翻转右侧链表,比较
快慢指针找中点,将慢指针置于中点或中点以左,快指针到末尾。翻转慢指针右侧节点,左侧子链表和右侧翻转过的两个链表进行比较,两链表的长度差值必须为1或0,相同位置元素必须相等。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* priv = nullptr;
ListNode* p = head;
while (p != nullptr) {
ListNode* nextTemp = p->next;
p->next = priv;
priv = p;
p = nextTemp;
}
return priv;
}
bool isPalindrome(ListNode* head) {
if (head->next == nullptr) {
return true;
}
ListNode* slow = head;
ListNode* fast = head;
while (fast != nullptr) {
if (fast->next != nullptr && fast->next->next != nullptr) {
fast = fast->next->next;
} else {
break;
}
slow = slow->next;
}
// slow为中点,slow下一个为头,fast做尾,翻转链表
ListNode* reverseHead = slow->next;
slow->next = nullptr;
ListNode* newSubList = reverseList(reverseHead);
ListNode* p = head;
ListNode* q = newSubList;
while (p != nullptr && q != nullptr) {
if (p->val != q->val) {
return false;
}
p = p->next;
q = q->next;
if (p == nullptr && q != nullptr && q->next != nullptr) {
return false;
}
if (q == nullptr && p != nullptr && p->next != nullptr) {
return false;
}
}
return true;
}
};
思路3 将链表值复制到数组,双指针比较
class Solution {
public:
bool isPalindrome(ListNode* head) {
vector<int> vals;
while (head != nullptr) {
vals.emplace_back(head->val);
head = head->next;
}
for (int i = 0, j = (int)vals.size() - 1; i < j; ++i, --j) {
if (vals[i] != vals[j]) {
return false;
}
}
return true;
}
};
删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
提示:
链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz
进阶:你能尝试使用一趟扫描实现吗?
思路1
首先特判长度为1的,直接返回空。如果长度大于1,使用map记录下下标和每个节点的地址,遍历一遍后,通过 count 长度,和 n 值,算出需要删除节点index的上一个节点的地址,注意如果删除的是第一个,直接返回 head->next .
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
if (head->next == nullptr)
return nullptr;
ListNode* p = head;
unordered_map<int, ListNode*> indexMap;
int count = 0;
while (p) {
indexMap[count++] = p;
p = p->next;
}
int index = count - n - 1;
if (index < 0) {
return head->next;
}
indexMap[index]->next = indexMap[index]->next->next;
return head;
}
};
官方题解
使用栈存储,弹出第n个就是需要删除的节点,此时再多弹出一个,就可以修改 next 指针来删除这个点。注意可以使用dummyHead哑节点,就不用对头节点特判了。
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummy = new ListNode(0, head);
stack<ListNode*> stk;
ListNode* cur = dummy;
while (cur) {
stk.push(cur);
cur = cur->next;
}
// 弹出第n个,再弹出一个,就是需要删除的节点的上一个
for (int i = 0; i < n; ++i) {
stk.pop();
}
// 将prev节点指向倒数第n个节点的下一个节点,即可实现删除
ListNode* prev = stk.top();
prev->next = prev->next->next;
ListNode* ans = dummy->next;
delete dummy;
return ans;
}
};
链表表示的两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
即数字 `435` ,表示为链表: `5->3->4`
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零
思路1
从头到尾遍历,两个链表相同位置的数是处于同等位上的数据,使用小学数学加法计算进位即可。使用 / 取商,使用 % 取余。控制好进位,最后如果最高位相加的结果除10不为0,即仍然需要进位,则需要加一个节点。
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* newHead = new ListNode(-1);
ListNode* q = newHead;
int carry = 0;
while (l1 || l2) {
int l1Value = l1 ? l1->val : 0;
int l2Value = l2 ? l2->val : 0;
int result = l1Value + l2Value + carry;
int thisNodeValue = result % 10;
ListNode* thisNode = new ListNode(thisNodeValue);
newHead->next = thisNode;
newHead = thisNode;
carry = result / 10;
if (l1)
l1 = l1->next;
if (l2)
l2 = l2->next;
}
if (carry > 0) {
newHead->next = new ListNode(carry);
}
return q->next;
}
};
这里刚刚编写的时候,在外面和循环里面都定义了一个int carry,二者命名相同没有报错,Java是会有报错的。后面需要注意这个特性。
删除排序链表中的重复元素
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
示例 1:
输入:head = [1,1,2]
输出:[1,2]
示例 2:
输入:head = [1,1,2,3,3]
输出:[1,2,3]
提示:
链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序 排列
思路
使用快慢指针,快指针一直往前检索重复值的节点,慢指针从头节点开始做比较,二者相同时,删除快指针所指的节点,不同时,慢指针移到快指针所在位置,快指针继续往前一步。
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
ListNode* fast = head->next;
ListNode* slow = head;
while (fast) {
while (fast != nullptr && (fast->val == slow->val)) {
ListNode* next = fast->next;
slow->next = slow->next->next;
fast = next;
}
slow = fast;
if (fast)
fast = fast->next;
}
return head;
}
};
官方题解优化复刻
不同于数组,刚刚编写时,总有一种感觉快慢指针咬的很紧,其实用不到快慢指针,本节点的next和本节点相同时,直接删除跳过即可。注意要防止遍历到最后一个节点时,调用current->next->val 报错的问题。
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
ListNode* current = head;
while (current->next) {
if (current->val == current->next->val) {
current->next = current->next->next;
} else {
current = current->next;
}
}
return head;
}
};
删除排序链表中的重复元素 II
给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表 。
示例 1:
输入:head = [1,2,3,3,4,4,5]
输出:[1,2,5]
示例 2:
输入:head = [1,1,1,2,3]
输出:[2,3]
提示:
链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序 排列
思路
这个变化的题和上一题在流程上类似,就是对比的值变成了这个节点的 next 和 next->next 。故也可以使用一个指针来判断,但是要注意元素从头开始就重复的情况,所以最好加虚拟头节点来辅助。
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if (!head) {
return head;
}
ListNode* dummy = new ListNode(0, head);
ListNode* cur = dummy;
while (cur->next && cur->next->next) {
if (cur->next->val == cur->next->next->val) {
int x = cur->next->val;
while (cur->next && cur->next->val == x) {
cur->next = cur->next->next;
}
} else {
cur = cur->next;
}
}
return dummy->next;
}
};
旋转链表
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
示例 1:
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]
示例 2:
输入:head = [0,1,2], k = 4
输出:[2,0,1]
提示:
链表中节点的数目在范围 [0, 500] 内
-100 <= Node.val <= 100
0 <= k <= 2 * 10^ 9
思路1 成环再掐断
先连成环,再从指定的位置断开。
例如长度为4,k为2,就需要从第二个节点往后断开,第二个节点作为尾节点,第三个节点为头。
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if (head == nullptr || head->next == nullptr) {
return head;
}
int count = 0;
ListNode* tail = head;
while (tail->next != nullptr) {
count++;
tail = tail->next;
}
count++;
// 需要掐断的第几个节点,从这里之后掐断
int breakPos = count > k ? count - k : count - (k % count);
// 二者相等,直接原地返回
if (breakPos == count) {
return head;
}
// 先成环再掐断
ListNode* p = head;
tail->next = head;
ListNode* newHead = p->next;
// p在头节点,移动到要断的这个节点
for (int i = 0; i < breakPos - 1; i++) {
p = p->next;
newHead = p->next;
}
p->next = nullptr;
return newHead;
}
};
官方代码
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if (k == 0 || head == nullptr || head->next == nullptr) {
return head;
}
int n = 1;
ListNode* iter = head;
while (iter->next != nullptr) {
iter = iter->next;
n++;
}
int add = n - k % n;
if (add == n) {
return head;
}
iter->next = head;
while (add--) {
iter = iter->next;
}
ListNode* ret = iter->next;
iter->next = nullptr;
return ret;
}
};
流程上一致,写法上更简洁精炼。
分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
示例 1:
输入:head = [1,4,3,2,5,2], x = 3
输出:[1,2,2,4,3,5]
示例 2:
输入:head = [2,1], x = 2
输出:[1,2]
提示:
链表中节点的数目在范围 [0, 200] 内
-100 <= Node.val <= 100
-200 <= x <= 200
思路1
使用快慢指针,快指针一直往前,负责需要前移的节点的拆除,慢指针永远指向小于这个值的最新节点,负责小节点的承接。最好加一个虚拟头节点,来防止第一个节点即属于大节点的情况。
class Solution {
public:
ListNode* partition(ListNode* head, int x) {
if (!head || !head->next)
return head;
// 使用头结点方便操作
ListNode *pre_node = new ListNode(-1), *pre = pre_node, *curr = pre;
pre_node->next = head;
// curr指向小于x的结点的前一个结点,pre指向小于值结点链的最后一个结点
while (curr && curr->next) {
// 将后链的小于值的结点摘下尾插前链中
if (curr->next->val < x) {
ListNode* tem = curr->next;
curr->next = tem->next;
tem->next = pre->next;
pre->next = tem;
// 当pre == curr时同时向后移动两个指针
if (curr == pre)
curr = curr->next;
pre = tem;
} else
curr = curr->next;
}
return pre_node->next;
}
};
官方题解
直观来说我们只需维护两个链表 small 和 large 即可,small 链表按顺序存储所有小于 x 的节点,large 链表按顺序存储所有大于等于 x 的节点。遍历完原链表后,我们只要将 small 链表尾节点指向 large 链表的头节点即能完成对链表的分隔。
为了实现上述思路,我们设 smallHead 和 largeHead 分别为两个链表的哑节点,即它们的 next 指针指向链表的头节点,这样做的目的是为了更方便地处理头节点为空的边界条件。同时设 small 和 large 节点指向当前链表的末尾节点。开始时 smallHead=small,largeHead=large。随后,从前往后遍历链表,判断当前链表的节点值是否小于 x,如果小于就将 small 的 next 指针指向该节点,否则将 large 的 next 指针指向该节点。
遍历结束后,我们将 large 的 next 指针置空,这是因为当前节点复用的是原链表的节点,而其 next 指针可能指向一个小于 x 的节点,我们需要切断这个引用。同时将 small 的 next 指针指向 largeHead 的 next 指针指向的节点,即真正意义上的 large 链表的头节点。最后返回 smallHead 的 next 指针即为我们要求的答案。
class Solution {
public:
ListNode* partition(ListNode* head, int x) {
ListNode* small = new ListNode(0);
ListNode* smallHead = small;
ListNode* large = new ListNode(0);
ListNode* largeHead = large;
while (head != nullptr) {
if (head->val < x) {
small->next = head;
small = small->next;
} else {
large->next = head;
large = large->next;
}
head = head->next;
}
large->next = nullptr;
small->next = largeHead->next;
return smallHead->next;
}
};
LRU缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示:
1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 105
最多调用 2 * 105 次 get 和 put
思路1
刚拿到有点懵,对于更新、插入、容量判断感觉还可以摸索实现,就是长期未用还不知如何实现。看到这张图,感觉就比较清晰了。触发过的往上移,那第一个节点就是最久未使用的。

LRU 缓存机制可以通过哈希表辅以双向链表实现,我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。
双向链表按照被使用的顺序存储了这些键值对,靠近头部的键值对是最近使用的,而靠近尾部的键值对是最久未使用的。
哈希表即为普通的哈希映射(HashMap),通过缓存数据的键映射到其在双向链表中的位置。
这样以来,我们首先使用哈希表进行定位,找出缓存项在双向链表中的位置,随后将其移动到双向链表的头部,即可在 O(1) 的时间内完成 get 或者 put 操作。具体的方法如下:
对于 get 操作,首先判断 key 是否存在:
如果 key 不存在,则返回 −1;
如果 key 存在,则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置,并将其移动到双向链表的头部,最后返回该节点的值。
对于 put 操作,首先判断 key 是否存在:
如果 key 不存在,使用 key 和 value 创建一个新的节点,在双向链表的头部添加该节点,并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量,如果超出容量,则删除双向链表的尾部节点,并删除哈希表中对应的项;
如果 key 存在,则与 get 操作类似,先通过哈希表定位,再将对应的节点的值更新为 value,并将该节点移到双向链表的头部。
上述各项操作中,访问哈希表的时间复杂度为 O(1),在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为 O(1)。而将一个节点移到双向链表的头部,可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作,都可以在 O(1) 时间内完成。
小贴士
在双向链表的实现中,使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限,这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
根据官方思想复刻
struct DoubleLinkedNode
{
int key;
int value;
DoubleLinkedNode *next;
DoubleLinkedNode *prev;
DoubleLinkedNode(int key, int value) : key(key), value(value), next(nullptr), prev(nullptr) {}
DoubleLinkedNode() : key(0), value(0), next(nullptr), prev(nullptr) {}
};
class LRUCache
{
private:
// map 的key存储的是节点的key, value存放指向节点地址的指针
unordered_map<int, DoubleLinkedNode *> dataMap;
DoubleLinkedNode *dummyHead = new DoubleLinkedNode(0, 0);
DoubleLinkedNode *dummytail = new DoubleLinkedNode(0, 0);
int tempSize = 0;
int capacity = 0;
public:
LRUCache(int _capacity)
{
capacity = _capacity;
dummyHead->next = dummytail;
dummytail->prev = dummytail;
}
int get(int key)
{
if (dataMap.count(key) > 0)
{
// 将查询过的节点移动到头部
moveToHead(dataMap[key]);
return dataMap[key]->value;
}
else
{
return -1;
}
}
void put(int key, int value)
{
// 判断存在性
if (dataMap.count(key) > 0)
{
// 修改节点的value值,移到最前
dataMap[key]->value = value;
moveToHead(dataMap[key]);
}
else
{
// 新建节点
DoubleLinkedNode *newNode = new DoubleLinkedNode(key, value);
// 添加进头部
addToHead(newNode);
// 添加进数据集
dataMap[newNode->key] = newNode;
tempSize++;
// 检查容量
if (tempSize > capacity)
{
removeTailNode();
tempSize--;
}
}
}
void moveToHead(DoubleLinkedNode *node)
{
removeNode(node);
addToHead(node);
}
void addToHead(DoubleLinkedNode *node)
{
node->next = dummyHead->next;
node->prev = dummyHead;
dummyHead->next->prev = node;
dummyHead->next = node;
}
void removeNode(DoubleLinkedNode *node)
{
node->next->prev = node->prev;
node->prev->next = node->next;
node->next = nullptr;
node->prev = nullptr;
}
void removeTailNode()
{
DoubleLinkedNode *tail = dummytail->prev;
// 删除数据集中的内容
dataMap.erase(tail->key);
removeNode(tail);
delete tail;
}
};
官方版本如下,在超出容量移除的时候,写法略有不同。
struct DLinkedNode {
int key, value;
DLinkedNode* prev;
DLinkedNode* next;
DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};
class LRUCache {
private:
unordered_map<int, DLinkedNode*> cache;
DLinkedNode* head;
DLinkedNode* tail;
int size;
int capacity;
public:
LRUCache(int _capacity): capacity(_capacity), size(0) {
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head->next = tail;
tail->prev = head;
}
int get(int key) {
if (!cache.count(key)) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
DLinkedNode* node = cache[key];
moveToHead(node);
return node->value;
}
void put(int key, int value) {
if (!cache.count(key)) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode* node = new DLinkedNode(key, value);
// 添加进哈希表
cache[key] = node;
// 添加至双向链表的头部
addToHead(node);
++size;
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode* removed = removeTail();
// 删除哈希表中对应的项
cache.erase(removed->key);
// 防止内存泄漏
delete removed;
--size;
}
}
else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
DLinkedNode* node = cache[key];
node->value = value;
moveToHead(node);
}
}
void addToHead(DLinkedNode* node) {
node->prev = head;
node->next = head->next;
head->next->prev = node;
head->next = node;
}
void removeNode(DLinkedNode* node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
void moveToHead(DLinkedNode* node) {
removeNode(node);
addToHead(node);
}
DLinkedNode* removeTail() {
DLinkedNode* node = tail->prev;
removeNode(node);
return node;
}
};
双链表对比单链表更不容易写断,可以先拆出来,再添加进去。将两边的同时要注意两个指针需要更新,next和prev两个都需要仔细操作;
拆分时将此节点的左右两个节点二指针互相连接即可。
添加时,需要将待添加位置的左右两个节点都指向这个节点,这个节点的next和prev也要指向插入位置左右的两个节点。
思路上很简单,更加考验代码细节设计编写。
